[컴퓨터비전] Backpropagation
🎀 해당 게시물은 국민대학교 김장호 교수님의 '컴퓨터비전' 강의를 수강하며 정리한 글입니다. 🎀
Gradients를 어떻게 계산할까?

경사하강법을 사용한 가중치 학습 과정을 설명하고 있다
손실 함수의 각 가중치 w_1, w_2에 대한 편미분을 계산하여 가중치를 업데이트할 것이다!!
나쁜 생각: 수작업으로 구해버려
이렇게 수작업으로 그라디언트를 계산하면?

- 행렬 미분 및 계산이 많아 수작업으로 수행하려면 상당한 시간이 소요된다
- 손실 함수를 바꾸고 싶을 때 처음부터 새로 유도해야한다.
- DNN이나 매우 복잡한 모델에서는 계산이 사실상 불가능하다고 한다..!
조은 생각: 계산 그래프를 사용해요!
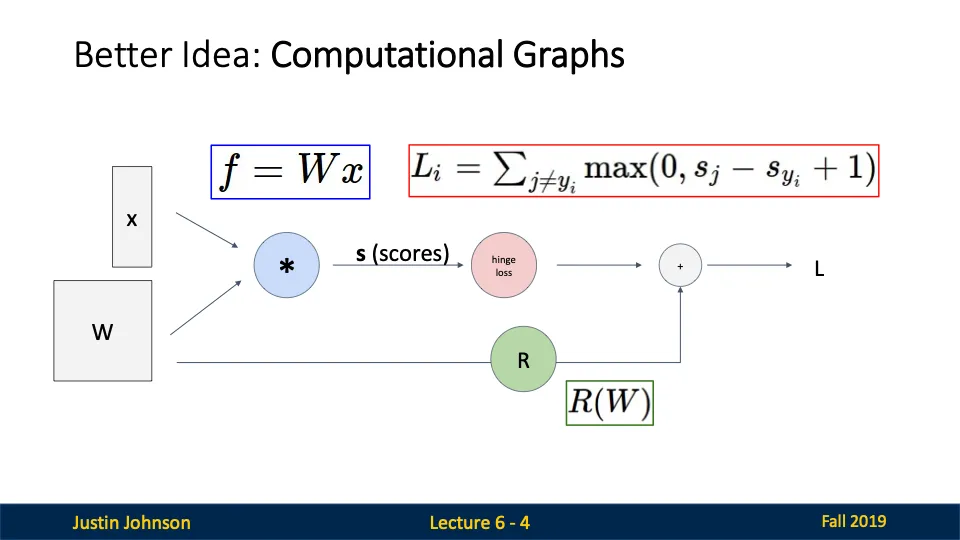
계산 그래프는 복잡한 함수를 구성하는 모든 연산 단계를 그래프로 나타낸다.
- 계산 흐름
- x와 W가 입력되고, 이들을 곱하여 점수 s를 계산합니다.
- 계산된 점수는 Hinge Loss 함수에 전달되어 손실 $L_i$를 계산합니다.
- 동시에 W는 정규화 항 R(W)를 계산하는 데 사용됩니다.
- 마지막으로 데이터 손실과 정규화 항을 더해 총 손실 L을 구합니다.
- 계산 그래프의 장점
- 모듈성
- 효율성: 역전파를 통해 노드의 그라디언트를 효율적으로 계산할 수 있다.
Backpropagation

역전파: 신경망의 각 레이어에서 효율적으로 그라디언트를 계산하여 경사 하강법을 실행할 수 있도록 지원
체인 룰: 복합 함수의 미분을 계산하기 위한 수학적 규칙
체인룰을 사용해서 그라디언트를 계산하였음!
Downstream Gradient = Local Gradient * Upstream Gradient

Upstream Gradient
이전(다음 층에서 전해주는) 그라디언트 값!이다.
손실 L이 최종 출력까지 미치는 영향을 나타낸다.
Local Gradient
해당 노드 내부에서 각 입력값 x와 y에 대해 출력 z가 얼마나 변하는지 계산한 값
Downstream Gradient
손실 L이 입력값 x, y 각각에 미치는 영향을 계산한 값
체인 룰을 통해 계산 된다!
활성화 함수의 그라디언트(미분 값)


sigmoid 함수의 그라디언트는 σ(x)(1−σ(x)) 이렇게 생겻는데, 큰 입력 값에서 기울기가 매우 작아지는 기울기 소실 문제가 있음
ReLU 함수의 그라디언트는 0보다 크거나 같을 때 1, 0보다 작을 때 0인데, 기울기가 0이 되면 죽은 뉴런 문제가 발생할 수도 있다.
이러한 문제를 해결한 것이 Leaky ReLU이다. 0보다 크거나 같을 때 1, 0보다 작을 경우에는 알파(작은 기울기 값)을 가진다.
Softmax 함수의 그라디언트

클래스 i와 j에 대해서 계산을 하는데 둘이 같을 때는 S_i(1 - S_i), 다른 클래스일 때는 -S_i S_j가 된다.
그라디언트 계산 꿀팁

- add gate: 그냥 그 숫자 그대로 전달
- mul gate: 반대쪽 숫자랑 곱해서 전달
- max gate: 더 큰쪽에 전달하고 다른 쪽에는 0 주기
역전파를 코드로 구현

