🎀 해당 게시물은 국민대학교 김장호 교수님의 '컴퓨터비전' 강의를 수강하며 정리한 글입니다. 🎀
Image Classification

이미지 분류(image Classification)은 고정된 카테고리 중 하나로 이미지를 분류하는 문제이다.
CIFAR-10

CIFAR-10은 이미지 분류를 위한 데이터셋이며, 다음과 같은 10개의 카테고리를 포함하고 있다.
각 이미지의 크기는 32*32*3이다. -> 3인걸 보니 RGB 채널인 것을 알 수 있다!
50,000장의 학습 데이터와 10,000장의 테스트 데이터로 분할되어있다!
Parametric Approach

선형 분류기는 학습 가능한 파라미터(가중치 W, 바이어스 b)를 사용한다.
입력이미지 x를 기반으로 클래스 점수 f(x, W)를 계산한다. (출력은 10개의 클래스 점수로 이루어진 벡터f(x,W)임)
- W: 학습 가능한 파라미터(모델이 학습을 통해 최적화)
- b: 클래스 간의 차이를 보정하는 역할(바이어스)
Algebraic Viewpoint

- 입력이미지: 2*2 크기의 이미지 → 열 벡터로 변환 (4, 1)
- 가중치 행렬: 각 행은 클래스(cat, dog, ship)에 대한 가중치 템플릿을 나타낸다.
- 바이어스 벡터: 각 클래스에 대해 추가적인 보정값을 제공한다.
- 출력: 3개의 클래스에 대한 점수가 반환된다. → 가장 높은 점수를 가진 클래스가 최종 예측 결과가 됨
Bias Trick

f(x, W) = Wx + b에서 바이어스 b는 별도로 계산되기 때문에 코드 구현이 번거로움
→ 입력 데이터에 1을 추가하고, 바이어스를 가중치 행렬 W의 마지막 열에 포함시킴
간단한 구현이 가능하고 계산 과정이 단순화되어 효율 업!
Predictions are Linear!

선형 분류기의 예측은 선형적 성질을 따른다!
쉽게 말하면 입력 이미지의 강도를 절반으로 줄이면, 출력 점수도 동일한 비율인 0.5배로 줄어든다는 것임
Visual VIewpoint

가중치 행렬의 각 행을 이미지 형태로 변환한여 특정 클래스의 템플릿으로 사용해버리기
모델이 학습한 특징을 시각적으로 이해할 수 있어서 좋음!
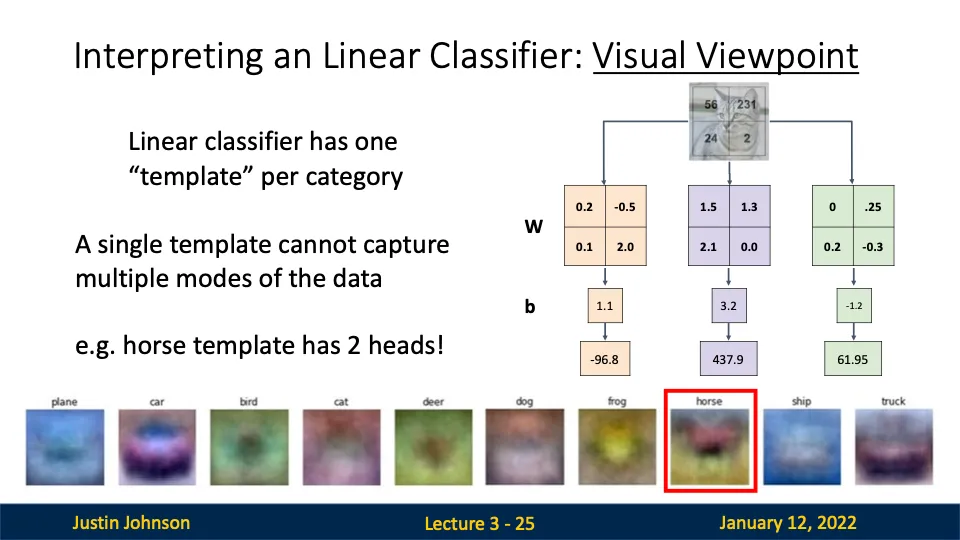
선형 분류기는 각 클래스에 대해 하나의 고유한 템플릿을 학습한다. (템플릿은 해당 클래스의 대표적인 특징을 강조함!)
이러한 템플릿과 입력 이미지와 얼마나 잘 맞는지를 계산하여 점수를 산출함
but!!!!!! 이러한 템플릿에는 한계가 존재함
- 단일 템플릿의 문제
- 하나의 템플릿으로는 데이터의 모든 변형과 다양성을 캡쳐할 수 없음
- ex) 말 템플릿의 2 heads 문제!!
- 다양성 부족
- 클래스마다 하나의 템플릿만 존재하므로, 데이터의 다양한 각도, 조명, 배경 등을 효과적으로 처리할 수 없다.
Perceptron은 왜 XOR 문제를 학습할 수 없나요..

perceptron은 선형 모델로 선형 분리 가능한 문제만 해결할 수 있다!
이러한 XOR 해결하기 위해서는 비선형성을 추가해야한다.
→ 다층 퍼셉트론(MLP, Multi-Layer Perceptron): 하나 이상의 은닉층(hidden layer)을 추가하여 비선형 결합을 학습.
Score function

점수 함수는 그냥 f(x, W) = Wx + b 식을 말한다고 생각하면 된다.
이 함수는 입력 이미지를 기반으로 각 클래스에 대한 점수를 계산한다.
W가 주어지면 점수를 계산할 수 있지만 어떤 W가 좋은 W일까?
→ 모든 데이터 포인트에 대해 손실(Loss Function)을 최소화 하는 W이다!!
- 손실 함수를 사용하여 W를 평가하자 (Cross-Entropy Loss)
- 최적화를 통해 손실 함수 값을 최소화는 W를 찾아보자 (손실함수의 기울기를 계산하고, Gradient Descent를 사용하여 W를 점진적으로 업데이트)
Loss Function

손실함수는 현재 분류기가 얼마나 좋은지 나쁜지 정량적으로 측정하는 도구이다.
- loss function = objective function(목적 함수) = cost function(비용 함수) = reward function = profit function
손실 값 (loss)
- 낮은 손실: 좋은 분류기
- 높은 손실: 나쁜 분류기
손실함수의 예시: Cross-Entropy Loss, Mean Squard Error(MSE)
+) 손실 함수 L을 최소화하기 위해, 경사하강법(GD) 같은 최적화 알고리즘을 사용한다.
Cross-Entropy Loss
선형 분류기의 출력 점수(스코어)를 Softmax 함수를 사용하여 확률로 변환하고 Cross-Entropy Loss함수를 통해 손실을 계산하는 과정을 보여줌

- 스코어 계산
- Unnormalized log-probabilities라고 불리는 선형 분류기의 출력점수들을 확률로 변환하기 위해 Softmax 함수를 사용할 것임
- Softmax함수를 사용하여 변환
- 확률의 총합이 1이 되도록 정규화 할 것임
- Cross-Entropy Loss 계산
- 정답 클래스에 -log()를 씌우면 됨 → 왜냐면 정답은 하나잔아!! 정답만 1을 곱해주고 나머지는 0을 곱하는 것이기 때문에 그냥 -log()안에 확률값을 넣어주면 끝인 것임
'Computer Vision' 카테고리의 다른 글
| [컴퓨터비전] Convolutional Networks (0) | 2024.12.22 |
|---|---|
| [컴퓨터비전] Vector Backpropagation (1) | 2024.12.22 |
| [컴퓨터비전] Backpropagation (2) | 2024.12.20 |
| [컴퓨터비전] Regularization (1) | 2024.12.19 |
| [컴퓨터비전] DNN(Deep Neural Network) (0) | 2024.12.19 |
