🎀 해당 게시물은 국민대학교 김장호 교수님의 '컴퓨터비전' 강의를 수강하며 정리한 글입니다. 🎀

문제점: 공간적 구조를 무시
고양이 Input image를 처리할 때, 픽셀 데이터를 벡터(1차원 배열)로 펼쳐 사용한다.
이 과정에서 이미지의 공간적 구조(픽셀 간의 위치 관계) 정보가 손실된다.
즉, 기존 신경망은 이미지의 공간적 특성을 학습하지 못하며 성능이 저하된다.
+) Fully-Connection Layer의 한계: 많은 계산량을 필요로함
해결책: 새로운 계산 노드(CNN) 도입
공간적 구조를 보존하는 새로운 계산 방식인, 합성곱 계층(Convolution Layer)가 등장!
CNN은 이미지 데이터의 공간적 관계를 학습하고, 중요한 특징(가장자리, 텍스처 등)을 추출할 수 있다!
- CNN의 효과
- 공간적 구조 반영: 이미지를 벡터로 변환하지 않고도 처리할 수 있다.
- 특징 학습: 필터를 통해 가장자리와 같은 국소적인 특징을 학습할 수 있다.
- 효율성: 계산량이 줄어든다.
Fully-Connected Network(완전 연결 신경망)의 구성요소
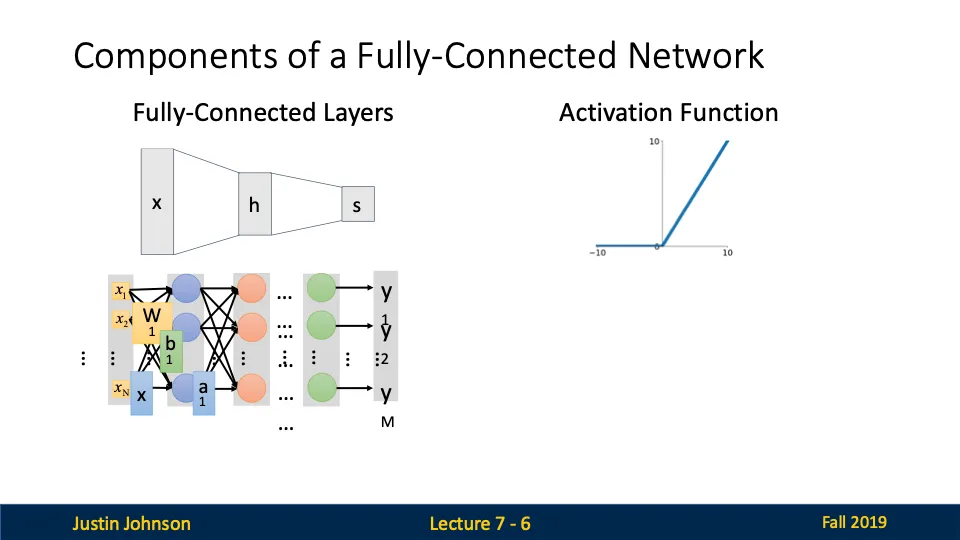
- Fully-Connected Layer(완전 연결 계층)
- Activation Function(활성화 함수): 활성화 함수는 신경망에 비선형성을 추가하여 더 복잡한 패턴을 학습할 수 있도록 한다.
다시말해, Fully-Connected Layer는 모든 뉴런이 연결된 단순한 구조를 가지고 있지만, 이미지 처리와 같은 공간적 정보를 고려해야 하는 경우 한계가 있기 때문에 이러한 한계를 극복하기 위해 CNN 도입
Fully-Connected Layer의 작동 방식
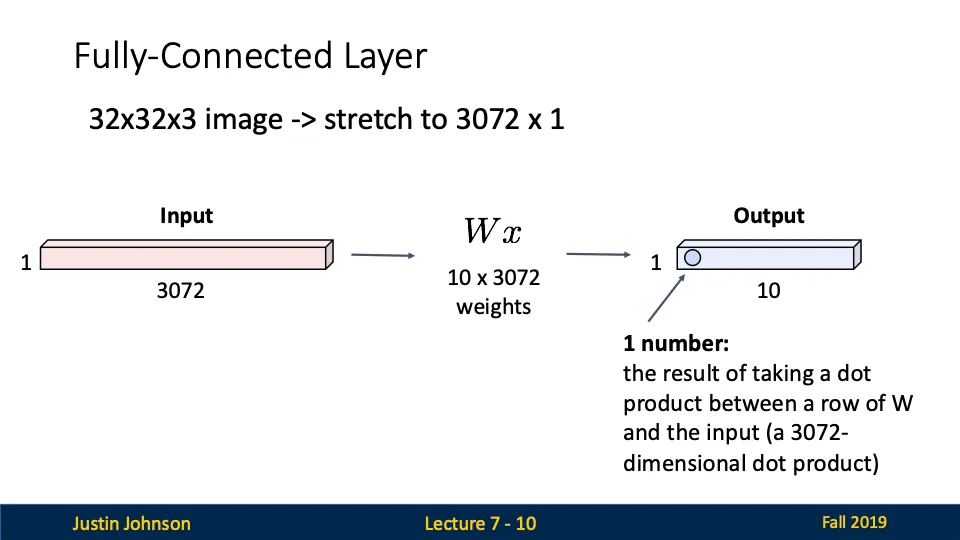
- input: 32*32*3 크기의 이미지를 벡터로 변환하여 32*32*3=3072 크기로 만듦
- 연산: W는 10*3072 크기의 행렬로 10차원의 output을 낸다.
- output: 10개의 값으로 구성된 벡터 (ex. 분류 문제에서 10개의 클래스에 대한 확률값)
Convolutional Layer의 작동 방식


- input: 3*32*32 크기의 이미지
- 3 = 입력 데이터의 채널 수
- 32*32 = 이미지의 높이와 너비
- filter: 3*5*5 크기의 필터(커널)
- 3 = 필터의 깊이는 항상 입력 데이터의 깊이와 동일
- 5*5 = 필터의 가로와 세로 크기
- 합성곱 연산
- 필터를 통한 연산: 필터가 입력 이미지 위에서 슬라이딩하며 작은 국소 영역마다 내적을 계산, w^Tx + b 형태로 계산
- 공간적 슬라이딩: 필터는 입력 이미지의 공간적 위치를 따라 슬라이딩하며 연산을 수행, 각 슬라이딩 위치에서 하나의 값이 계산됨
- output: 활성화 맵(Activation Map)이 출력된다.

Convolutional Layer의 계산을 일반화 해보자!



Stacking Convolution
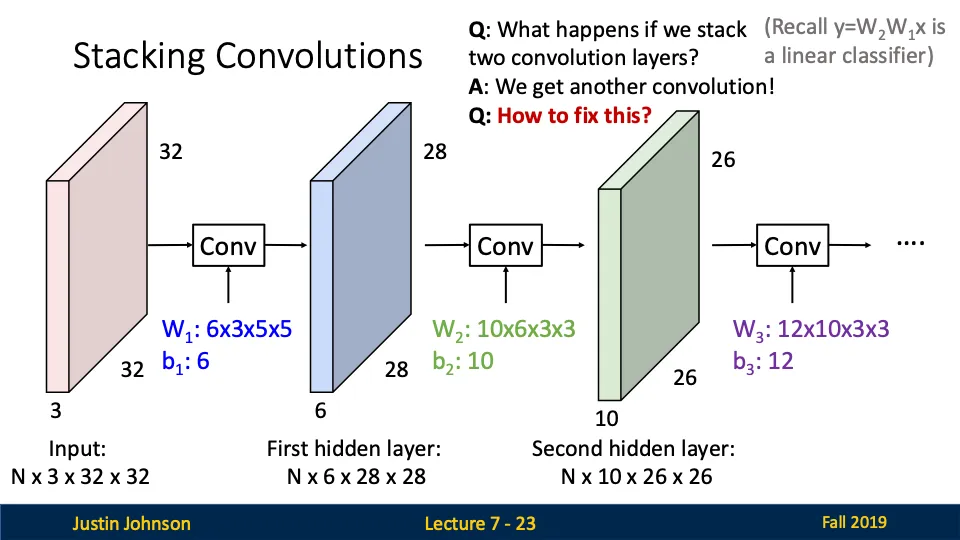
Q. 두 개 이상의 합성곱 계층을 쌓으면 우째요?
A. 합성곱 연산만 수행하면 결과는 여전히 선형적인 변환이다!

Q. 그럼 어케 복잡한 패턴을 학습 시켜요?
A. 활성화 함수를 사용하여 비선형성을 추가 시킨다!
앞서 다루었던 batch와 여러 필터를 사용하는 것이랑은 다르다!
| 개념 | 배치(Batch) | 필터를 여러 개 사용 | 합성곱 계층 쌓기 |
| 설명 | 여러 이미지를 동시에 처리 | 한 계층에서 여러 특징을 학습 | 여러 계층을 연결해 복잡한 특징 학습 |
| 목적 | 연산 효율성과 학습 속도 향상 | 다양한 특징을 학습 | 점진적으로 복잡한 정보 학습 |
| 예시 | N×C×H×W | 6개의 필터 → 6개의 활성화 맵 | 출력 맵이 다음 계층의 입력이 됨
|
A closer look at spatial dimensions
→ 합성곱 연산에서 공간적 차원이 어떻게 변화하는지 설명
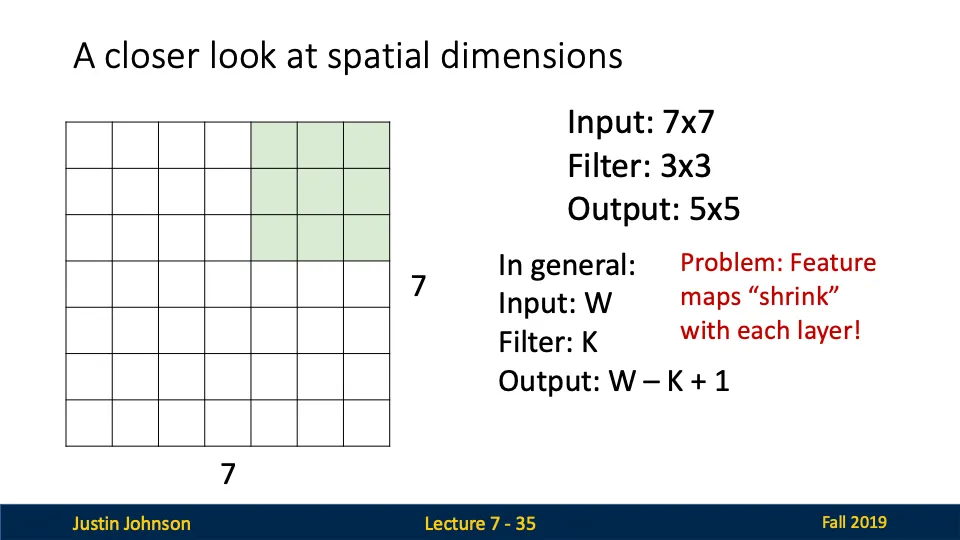
- 출력 크기 계산 공식
- output size = input size - filter size + 1
- 7 - 3 + 1 = 5
- 문제점: 출력 크기 감소
- 각 합성곱 계층을 거칠 때마다 출력 크기가 줄어둔다.
- 7*7 → 5*5 → 3*3 → 1*1
- 즉, 계층이 많아질수록 데이터가 빨리 축소되며, 너무 작은 출력은 정보 손실을 초래함!
- 각 합성곱 계층을 거칠 때마다 출력 크기가 줄어둔다.

- 해결방법: 패딩을 사용한다!!!!
- 입력 이미지의 가장자리에 0을 추가하여 출력 크기가 줄어드는 것을 방지한다.
- 패딩 후 크기 = 9*9
- 필터 크기 3*3을 적용한 후 출력 크기 = 9-3+1 = 7 → 패딩 덕분에 출력 크기가 입력 크기와 동일해진다.

그렇다면 출력 크기가 입력 크기와 동일하게 유지되도록 패딩 값을 설정하려면 우째해요?
패딩의 크기는 (K-1)/2 로 필터 크기의 절반!!입니다.
Receptive Fields (수용 영역)
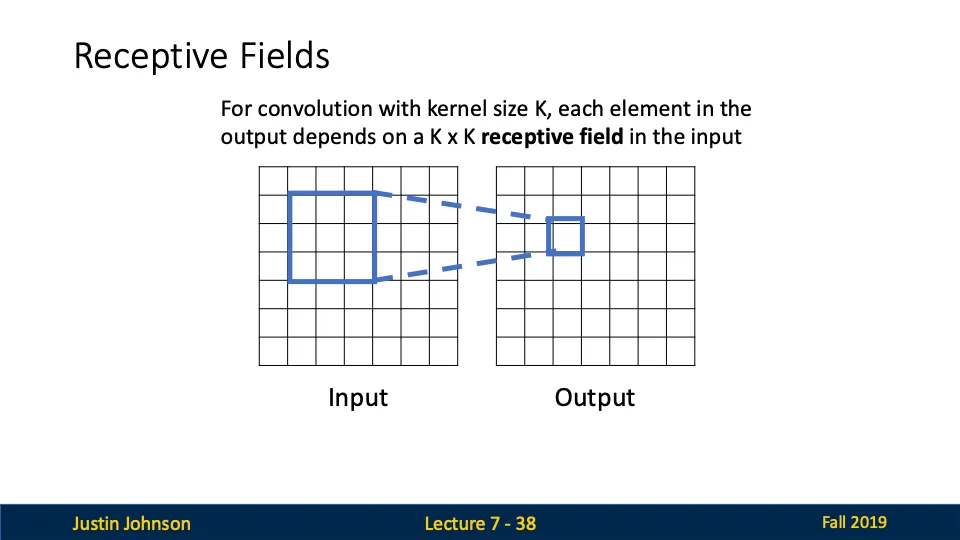
Receptive Field의 개념
- Receptive Field: 각 출력 뉴런이 입력 이미지에서 영향을 받는 영역
- 합성곱 계층에서 출력의 각 픽셀은 입력 이미지에서 특정 영역(Receptive Field)에 의해 결정됨
- 필터 크기 K*K는 Receptive Field의 크기를 정의
- 역할
- 출력의 각 픽셀이 입력의 일부 국소적 영역에 영향을 받습니다.
- 국소적 특징(가장자리, 텍스처)을 학습할 수 있게 됩니다.

Receptive Field의 확장
- Receptive Field가 확장되는 과정:
- 계층이 깊어질수록 각 출력 픽셀이 입력에서 영향을 받는 영역(Receptive Field)이 커집니다.
- 예를 들어, 두 번째 계층의 각 픽셀은 이전 계층에서 더 넓은 영역을 수용합니다.
- Receptive Field 크기 계산 공식:
- Receptive Field Size = 1+L×(K−1)
- L: 계층 수
- K: 필터 크기
- Receptive Field Size = 1+L×(K−1)
Receptive Field의 문제점
이미지가 클수록 모든 출력 픽셀이 이미지 전체를 볼 수 있는 Receptive Field를 가지려면 많은 계층이 필요하다.
(더 깊은 계층으로 갈 수록 영역이 커지면서 출력의 한 픽셀이 보는 영역이 넓어진다는 의미)
즉, Receptive Field가 느리게 확장되므로 네트워크가 입력 전체를 이해하기 어렵다.
→ 네트워크의 연산량이 증가하고 학습속도 느려짐
→ 정보 손실없이 Receptive Field를 넓히기 어려움
Receptive Field의 해결책
- 네트워크 내에서 Downsampling(크기 축소)을 통해 Receptive Field를 더 빠르게 확장.
- 일반적으로 Pooling 계층(Max Pooling 등)이나 Strided Convolution(스트라이드 합성곱)을 사용.
- 효과:
- Downsampling을 통해 공간적 크기를 줄이고 Receptive Field 확장을 가속화.
- 예를 들어, Pooling 계층을 사용하면 출력 크기가 절반으로 줄어듭니다.
- 결과:
- 각 출력 뉴런이 더 넓은 영역을 볼 수 있게 되어, 입력 전체를 이해하는 데 필요한 계층 수가 감소합니다.
Strided Convolution (스트라이드 합성곱)

- Stride: 필터를 입력 위에서 얼마나 건너뛰면서 적용할지를 나타내는 값
- 기본적인 합성곱에서는 s = 1 사용(한칸씩 이동한다는 뜻)
- s = 2 라면? 필터가 두 칸씩 건너 뛰며 계산을 하게 됩니다~
- 출력 크기 공식

- stride의 장점
- 출력 크기가 감소한다.(계산량 줄고, 모델 효율성은 높아짐)
- Receptive Field가 빠르게 확장됨
- stride의 단점
- 정보 손실: 필터가 입력을 건너뛰면서 적용되므로!
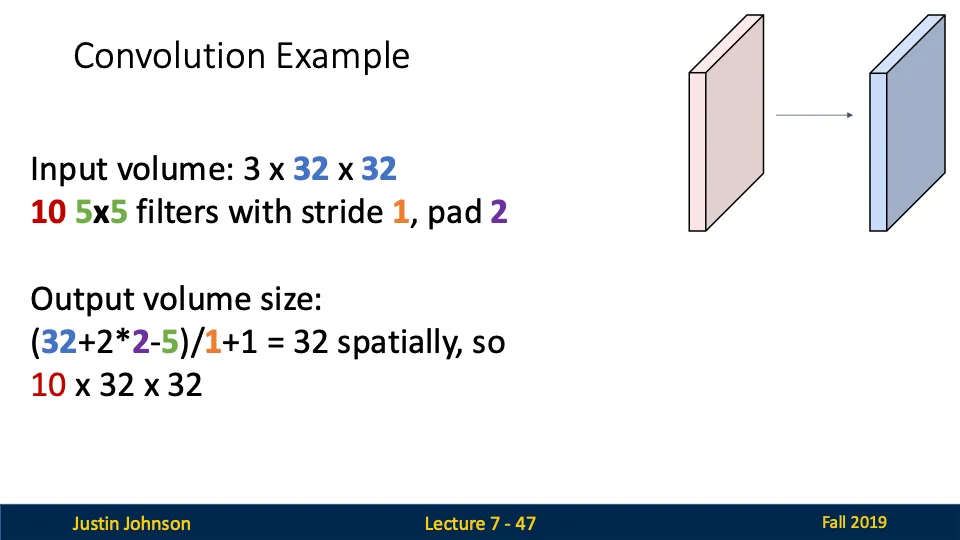
Convolution Example - 출력 크기 계산

Convolution Example - 학습 가능한 매개변수 수


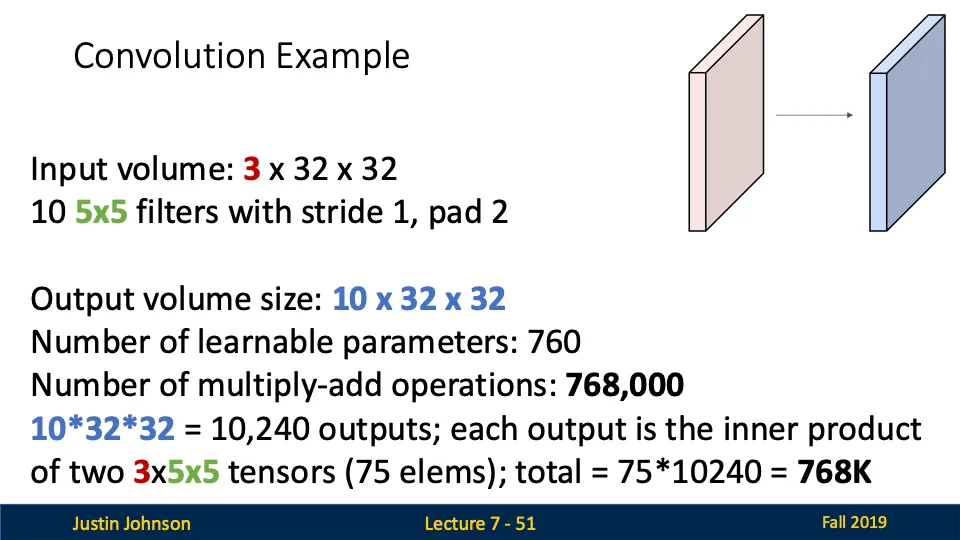
Convolution Example - 연산량 계산

'Computer Vision' 카테고리의 다른 글
| [컴퓨터비전] Vector Backpropagation (1) | 2024.12.22 |
|---|---|
| [컴퓨터비전] Backpropagation (2) | 2024.12.20 |
| [컴퓨터비전] Regularization (1) | 2024.12.19 |
| [컴퓨터비전] DNN(Deep Neural Network) (0) | 2024.12.19 |
| [컴퓨터비전] Linear Classifiers (0) | 2024.12.19 |
