🎀 해당 게시물은 국민대학교 김장호 교수님의 '컴퓨터비전' 강의를 수강하며 정리한 글입니다. 🎀
Supervised learning (지도 학습)
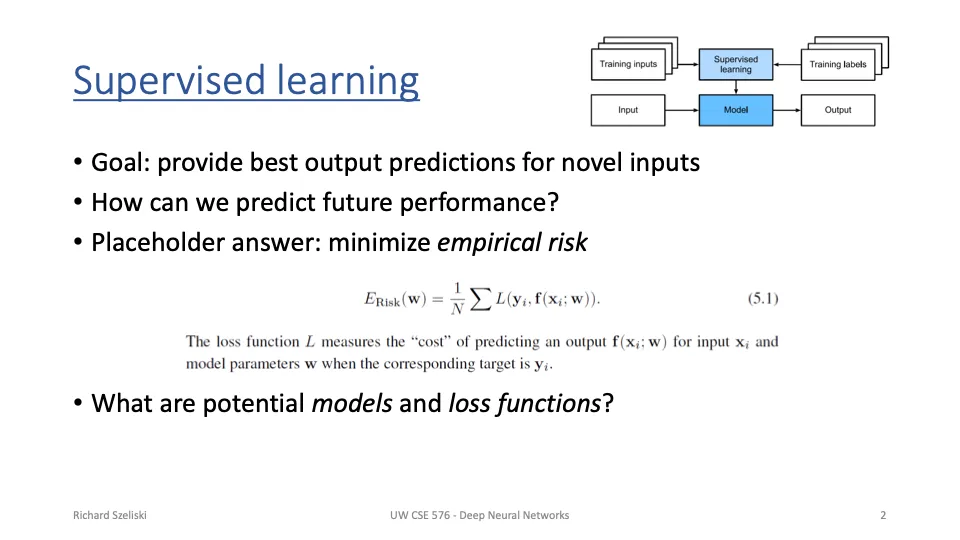
- 지도학습의 목표: 새로운 입력 데이터에 대해 가장 정확한 출력 예측을 제공
- 미래의 성능을 어떻게 예측할 수 있을까?
- 경험적 위험(실제 데이터에서의 평균 손실)을 최소화한다.
→ 모델이 학습 데이터뿐만 아니라 보지 않은 새로운 데이터에서도 잘 작동해야한다!
- 경험적 위험(실제 데이터에서의 평균 손실)을 최소화한다.
Deep learning

| 구분 | 전통적 비전 파이프라인 | 고전적 머신러닝 | 딥러닝 |
| 특징 추출 | 사람이 설계 | 사람이 설계 | 자동 학습 (CNN) |
| 학습 알고리즘 | 없음 (수작업 알고리즘 사용) | 머신러닝 알고리즘 | 딥러닝 모델 자체가 수행 |
| 장점 | 간단하고 직관적 | 다양한 알고리즘 지원 | 높은 표현력과 적응력 |
| 단점 | 확장성 부족 | 특징 추출의 한계 | 높은 계산 비용 |
딥러닝은 특징 추출과 학습이 완전히 자동화된 것이다.
Cross-Entropy Loss(다항 로지스틱 회귀*)


- KL Divergence는 Q와 P의 차이를 정량화하며, Cross-Entropy Loss에 포함되어 있.
- Cross-Entropy Loss를 최소화하는 것은 KL Divergence를 최소화하는 것과 같고, 모델이 정답 클래스에 더 높은 확률을 할당하도록 만드는 과정이다.
💡다항 로지스틱 회귀*: 입력 데이터를 여러 클래스 중 하나로 분류
Neural Networks
linear Classifier의 한계

- 데이터가 선형적으로 분리 가능하지 않은 경우, 선형 분류기는 제대로 작동하지 않는다
→ 위의 그림처럼 클래스가 원형으로 배치된 경우, 단일 직선으로 이들을 분리할 수 없다.(XOR) - 선형 분류기는 각 클래스에 대해 하나의 템플릿만 학습하기 때문에 모양이 쪼꼼만 달라져도 분류를 못할 수도 있다!(말의 2 heads problem)
해결책: Feature Transforms(특징 변환)
- 데이터를 다른 공간으로 변환하여 선형적으로 분리 가능하도록 만드는 기법

원래 공간에서는 데이터가 선형적으로 분리 불가능하다.
그러나 feature transform을 통해 데이터를 다른 공간으로 변환하여 선형적으로 분리 가능하게 만들 수 있다.
변환된 데이터는 특징 공간에 위치하게 되며, 원래 공간에서 비선형적으로 분포된 데이터도 특징 변환을 통해 선형적으로 분리 가능하게 된다!
Neural Networks (신경망)

- 선형 점수 함수
- 선형 모델은 데이터가 선형적으로 분리 가능한 경우에만 제대로 작동
- 복잡한 데이터 분포를 학습할 수 없음
- 신경망 구조
- 2-layer Neural Network (2개의 층을 가진 신경망)
- 층(layer)을 추가하고 활성화 함수를 적용하면, 선형적으로 분리 불가능한 데이터도 학습 가능.
- 장점
- 표현력 강화: 다층 구조와 활성화 함수로 비선형 데이터를 처리할 수 있다.
- 복잡한 데이터 분포 학습: 더 많은 은닉층과 뉴런을 추가하면 더 복잡한 데이터 구조를 학습 가능
- End-to-End 학습: 입력에서 출력까지 모든 과정에서 가중치와 편향을 학습
Activation Functions(활성화 함수)

- 활성화 함수란?
- 신경망의 각 층(layer) 사이에서 입력 값을 변환하여 비선형성을 도입하는 함수
- ex) ReLU → 입력값이 음수일 경우 0, 양수일 경우 그대로 반환
- 활성화 함수가 없는 경우에는 어떻게 될까?
- 각 층의 선형 변환이 결합되어 최종적으로 하나의 선형 변환!!!!이 된다.
- 복잡한 데이터의 비선형 관계를 학습할 수 없다.
Fully-Connected Neural Network (MLP)

- Fully-Connected Neural Network (다층 퍼셉트론, MLP)
- 각 입력 노드가 은닉층의 모든 노드와 연결되어 있는 구조 + 은닉층의 모든 노드가 출력층의 모든 노드와 연결됨
- 각 층에서 모든 노드가 연결되어 있으므로 데이터의 상호작용이 극대화 된다.
→ 모든 입력이 모든 출력에 영향을 미침
Distributed Representation (분산 표현)

- 선형 분류기의 한계
- 선형 분류기는 클래스당 하나의 템플릿만 생성할 수 있다.
→ 말의 모양은 다양한데 선형분류기는 이를 하나의 템플릿으로만 처리한다.
- 선형 분류기는 클래스당 하나의 템플릿만 생성할 수 있다.
- 2-layer Neural Network의 표현 능력
- 은닉층에서 여러 템플릿을 생성하여 클래스의 다양한 모드를 학습한다
- Neural net
- 첫 번째 은닉층: 다양한 템플릿을 학습 (템플릿 은행, Bank of Templates)
- 두 번째 은닉층: 이 템플릿들을 조합하여 최종 클래스를 예측
- Distributed Representation
- 은닉층의 템플릿들은 대부분 명확히 해석할 수 없는 분산표현을 형성한다.
→ 각 템플릿이 특정한 고유한 의미를 갖지 않고, 여러 템플릿이 함께 조합되어 의미를 만든다는 것이다~ (이로 인해 신경망이 더 복잡한 패턴을 학습할 수 있음)
- 은닉층의 템플릿들은 대부분 명확히 해석할 수 없는 분산표현을 형성한다.
⇒ 이렇게 말 머리 두개 문제 해결함 ㅋ
Deep Neural Networks

- Depth: 네트워크의 층 수
- Width: 각 층의 뉴런(노드) 개수
'Computer Vision' 카테고리의 다른 글
| [컴퓨터비전] Convolutional Networks (0) | 2024.12.22 |
|---|---|
| [컴퓨터비전] Vector Backpropagation (1) | 2024.12.22 |
| [컴퓨터비전] Backpropagation (2) | 2024.12.20 |
| [컴퓨터비전] Regularization (1) | 2024.12.19 |
| [컴퓨터비전] Linear Classifiers (0) | 2024.12.19 |
