🎀 해당 게시물은 국민대학교 김장호 교수님의 '컴퓨터비전' 강의를 수강하며 정리한 글입니다. 🎀

이전 선형 모델에서 2층 신경망으로 바뀌면서 복잡한 데이터 패턴을 학습할 수 있도록 하였음
이전에는 직선으로 반반 나누는 것들 밖에 못했는데 이제는 XOR 연산을 할 수 있게 된 것!

- Width: 각 층에 있는 뉴런의 개수
- Depth: 깊이 = 은닉층 + 출력층 = 6+1 = 7
Loss Function

- loss function은 현재 모델이 얼마나 잘 작동하는지 평가하는 기준임
- 대표적인 손실함수에는 MSE와 cross-entropy loss 가 있음
오버피팅

- 새로운 데이터에 대한 일반화(generalize) 성능이 낮아지는 것을 의미한다.
- 학습데이터의 패턴뿐만 아니라 노이즈까지 학습하여 모델이 학습데이터에 대해 지나치게 잘 맞추는 상태
오버피팅 방지 방법
(1) 데이터 관련 방법
- 더 많은 데이터 수집: 모델이 일반화할 수 있도록 다양한 데이터를 제공.
- 데이터 증강(Data Augmentation): 기존 데이터를 변형하여 학습 데이터의 다양성을 늘림.
(2) 모델 관련 방법
- 모델 단순화: 파라미터 수를 줄이거나 모델의 복잡도를 낮춤.
- 정규화(Regularization):
- L1 또는 L2 정규화를 통해 가중치를 제한하여 복잡도를 낮춤.
- 드롭아웃(Dropout):
- 학습 중 일부 뉴런을 무작위로 비활성화하여 과적합 방지.
(3) 학습 과정 관련 방법
- 조기 종료(Early Stopping):
- 검증 데이터의 성능이 더 이상 개선되지 않을 때 학습을 멈춤.
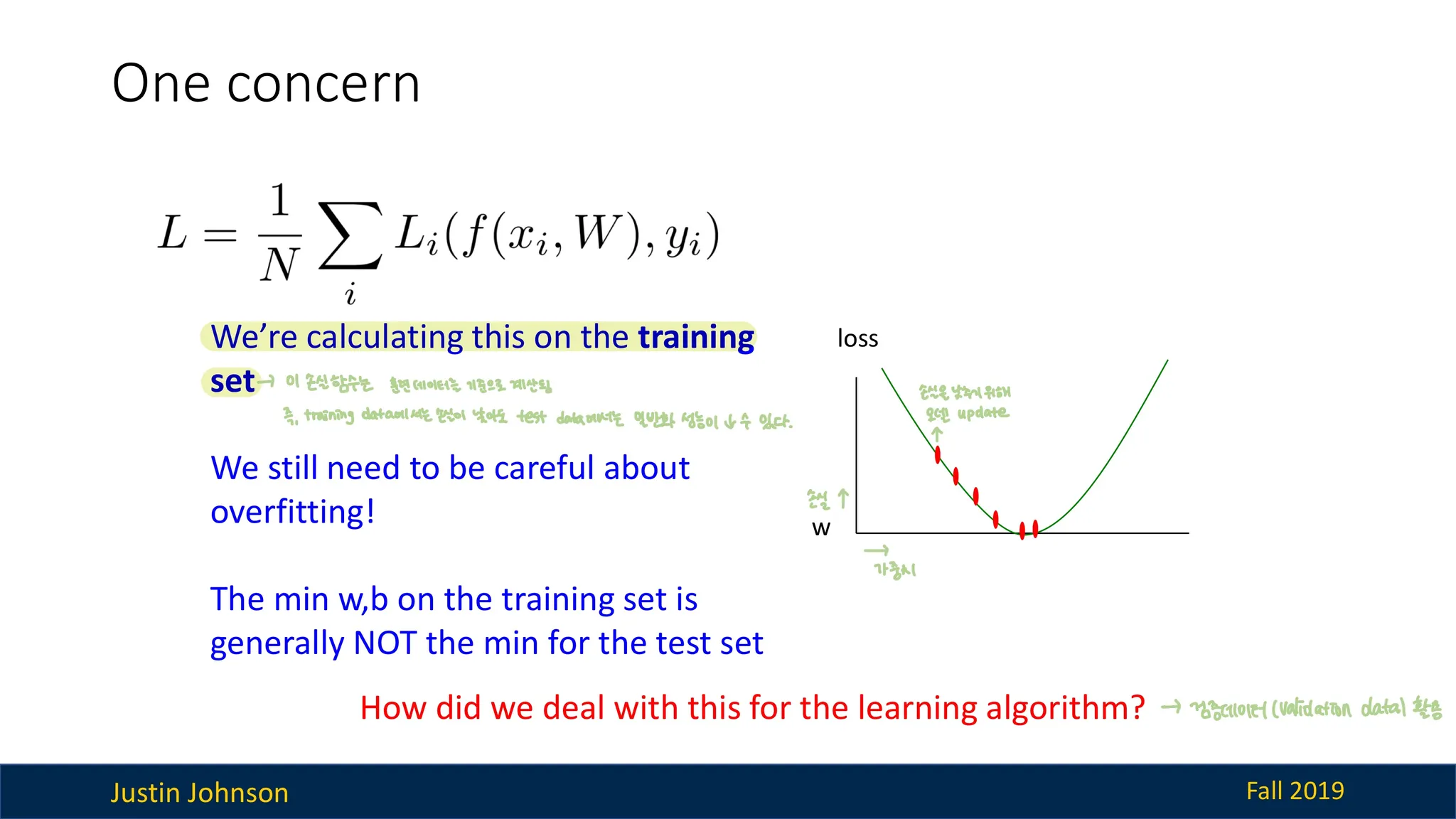
그러나 위의 손실함수는 훈련 데이터(training data)를 기준으로 계산된다.
즉, 훈련 데이터에 대해서는 loss가 낮더라도 테스트 데이터에 대해서는 loss가 높을 수 있음
이에 대한 해결 방법에는 4가지가 있다. (= 오버피팅 방지 방법과 같음)
- 검증 데이터(validation set) 활용
- 데이터를 훈련/검증/테스트 세트로 나눈다.
- 훈련 데이터: 모델 학습.
- 검증 데이터: 모델의 성능 평가 및 조정(하이퍼파라미터 튜닝).
- 테스트 데이터: 최종 평가.
- 검증 데이터에서 손실 값이 더 이상 줄어들지 않을 때 학습을 멈추는 조기 종료(Early Stopping) 기법을 사용
- 데이터를 훈련/검증/테스트 세트로 나눈다.
- 정규화(Regularization)
- 모델의 복잡도를 줄여서 오버피팅을 방지
- L1/L2 정규화를 통해 가중치가 너무 크거나 복잡해지지 않도록 제한함
- 모델 단순화
- 뉴런 개수나 레이어 수를 줄여 과도한 학습을 방지
→ 간단한 모델은 오버피팅의 가능성을 낮춤
- 뉴런 개수나 레이어 수를 줄여 과도한 학습을 방지
- 데이터 증강(Data Augmentation)
- 기존의 데이터를 변형하여 데이터 다양성을 높임
정규화(Regularization)
- 손실 함수에 추가적인 항목(regularizer)을 더해 과적합(overfitting)을 방지하는 방법
- 목적: 모델이 학습 데이터에만 너무 오버피팅되지 않고 새로운 데이터에 대해 더 잘 일반화(generalize)할 수 있도록 돕는 것
정규화 수식

- $\sum_{i=1}^{n} \text{loss}(y_i, \hat{y}_i)$:
- 손실 함수로, 예측값(y^i)과 실제값(yi) 간의 차이를 계산.
- 이 항목은 모델의 정확도를 높이는 데 중점을 둡니다.
- regularizer(w,b):
- 정규화 항목으로, 모델의 가중치와 바이어스를 제한하여 과적합을 방지.
- 일반적으로 L1, L2 정규화와 같은 형태를 사용합니다.
- λ:
- 정규화 강도를 조절하는 하이퍼파라미터.
- λ가 클수록 정규화 효과가 커집니다(가중치를 더 강하게 제한).
- 목적: 손실 값(데이터 적합도)과 정규화 항목(모델 단순성)의 균형을 찾는 것
정규화의 목적

- 모델 선호도 표현: 훈련 오류를 최소화하는 것이 아니라, 더 단순하고 일반화된 모델을 선호하도록 유도
- 오버피팅 방지: 모델이 훈련데이터에만 과적합되지 않도록, 간단한 모델을 선호하게 만듦
- 최적화 개선: 정규화는 손실함수에 곡률을 추가하여 최적화 과정을 원활하게 만듦
즉, 훈련 데이터만 고려하는 학습은 오버피팅을 유발할 가능성이 높으므로 정규화를 통해 모델의 복잡성을 제어함으로써 테스트 데이터에서도 좋은 성능을 발휘하도록 만든다!!!!
정규화가 가중치에 미치는 영향과 그 이유는?

이 수식 f=Wx 은 단순한 선형 모델을 표현한다.
그렇다면 왜 큰 가중치는 피해야할까?
큰 가중치는 입력 데이터의 작은 변화도 예측값에 큰 영향을 미친다. 즉, 모델이 데이터의 노이즈까지 학습할 가능성이 높아진다.
또한 사용되지 않거나 중요하지 않은 입력(feature)에 대해서는 가중치는 0으로 설정하는 것이 효과적이다.
그렇다면 어떻게하면 작은 가중치를 유도하고, 큰 가중치에 패널티를 부여할 수 있을까?

(1) L2 정규화 (Ridge Regression)
- 수식: $\lambda \sum w^2$
- 가중치 w의 제곱합을 손실 함수에 추가.
- 효과:
- 가중치가 클수록 큰 페널티를 부과하여 가중치를 작게 유지.
- 모든 가중치가 조금씩 감소하는 경향.
(2) L1 정규화 (Lasso Regression)
- 수식: $\lambda \sum |w|$
- 가중치 w의 절댓값 합을 손실 함수에 추가.
- 효과:
- 일부 가중치를 정확히 0으로 만들어 중요하지 않은 특징(feature)을 제거.
- 특징 선택(feature selection)에 유리.
(3) Elastic Net
- L1과 L2 정규화를 결합한 방식.
- 모델이 데이터에 따라 L1/L2 정규화의 장점을 모두 활용.
+) 복잡한 정규화 기법:
- Dropout: 학습 중 무작위로 뉴런을 끄는 방식으로 과적합을 방지.
- Batch Normalization: 데이터 분포를 정규화하여 학습 안정화.
- Cutout, Mixup, Stochastic Depth 등: 추가적인 데이터 증강 및 네트워크 변형 기법.
L2 Regularization: Weight Decay

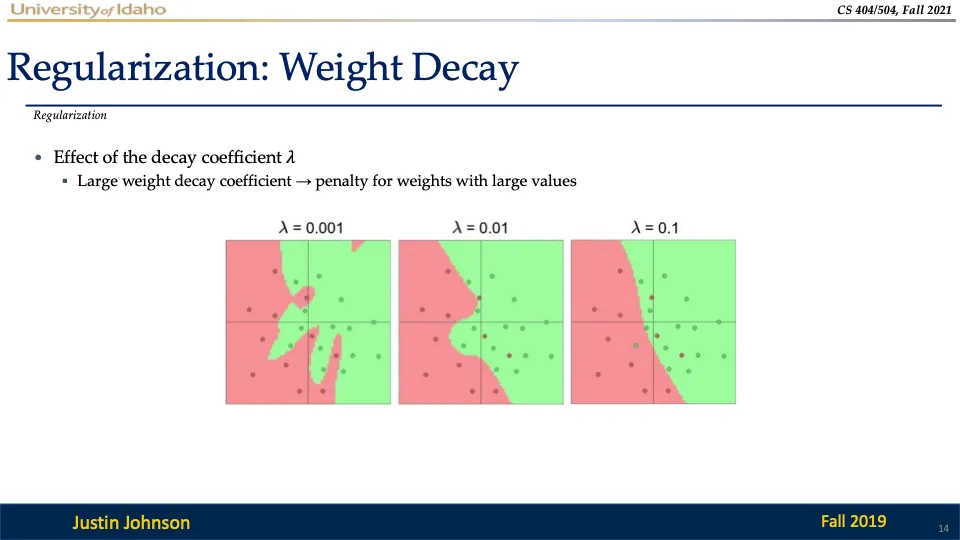
L2 정규화는 Ridge 회귀로도 알려져 있으며, 손실 함수에 큰 가중치 값을 억제하기 위한 항을 추가하는 정규화 방법이다!
- 작동원리
- 네트워크의 각 가중치에 대해 정규화 항이 손실 값에 추가된다.
- 경사하강법 과정에서 매번 매개변수 업데이트 시, 각 가중치가 0에 더 가까워지도록 선형적으로 감쇠(decay)된다.
- 정규화 계수(λ): 정규화 강도를 조절하는 하이퍼파라미터
- 작을수록: 정규화가 미미하게 적용되어 데이터에 더 과적합될 가능성이 높음
- 클수록: 정규화 효과가 강해져, 모델이 과도하게 단순화될 위험
L1 Regularization & Elastic Net

L1 정규화는 일부 가중치를 0으로 만드는데(희소성 촉진) 효과적이지만 뉴럴 네트워크에서 L2 정규화보다 성능이 떨어지는 경우가 많다.
Elastic Net 정규화는 L1의 희소성 효과와 L2의 일반화 성능을 결합한 방식임
모델 기반 머신러닝(Model-based Machine Learning)

Model-based Machine Learning이란?
- 머신러닝에서 모델을 기반으로 학습하는 접근 방식입니다.
- 목표: 데이터를 가장 잘 설명하는 모델의 파라미터(가중치 w, 바이어스 b)를 찾는 것입니다.
- ∥𝑤∥ : 모든 벡터를 제곱하여 더한 값에 루트를 씌운 것..
- 모델 선택: 적절한 수학적 구조로 데이터 표현
- 최적화 기준: 데이터 적합성과 모델의 일반화 성능 사이의 균형
- 학습 알고리즘: 목표는 손실을 최소화하면서 일반화 가능한 모델을 만드는 것
Optimization Criterion (최적화 기준)

- Loss Function
- 모델의 예측값이 실제 레이블과 다를 때 패널티를 부여한다.
- y_i는 데이터의 실제 레이블입니다.
- w * x_i + b는 예측된 값입니다.
- 예측값이 실제 레이블과 멀어질수록 손실이 증가합니다.
- 모델의 예측값이 실제 레이블과 다를 때 패널티를 부여한다.
- Regularizer
- 너무 큰 가중치를 패널티로 제한하여 모델이 과적합되지 않도록 방지
중요! 이 함수는 볼록(convex)이므로, 경사하강법을 사용해서 최적화 할 수 있다!
Gradient Descent(경사하강법)
Gradient Descent는 최적화 문제를 풀기 위해 사용됩니다. 즉, 모델의 손실(loss)을 최소화하기 위해 가중치 w와 편향 b를 업데이트하는 방법

경사하강법 과정
- 초기값 설정: 가중치 w의 초기값을 설정한다(무작위)
- 반복 작업
- 손실 함수의 값을 계산
- 손실 함수의 기울기를 계산
- 기울기를 따라 가중치를 조금씩 업데이트

목적함수 미분하기

목적 함수의 기울기 계산은 각 가중치인 w에 대해 미분을 하면 된다.
손실함수에 대해 기울기 계산하고, 정규화 항에 대해 기울기 계산하면 저 아래 처럼 계산이 된다.
경사하강법 업데이트 식

L2 정규화와 경사하강법 효과

- 가중치 w_j가 양수일 경우, 감소시켜서 0에 가깝게 만듦.
- 가중치 w_j가 음수일 경우, 증가시켜서 0에 가깝게 만듦.
⇒ 결과적으로, 가중치를 0으로 수렴시킴으로써 불필요한 가중치를 제거하고 모델을 단순화. (0이 되는 것은 아님)
L1 정규화와 경사하강법 효과

- 가중치가 양수일 경우 일정 값을 감소시킵니다.
- 가중치가 음수일 경우 일정 값을 증가시킵니다.
- 이는 가중치를 크기에 상관없이 점진적으로 0으로 이동시키는 효과를 가져옵니다. (아예 0으로)
행렬연산
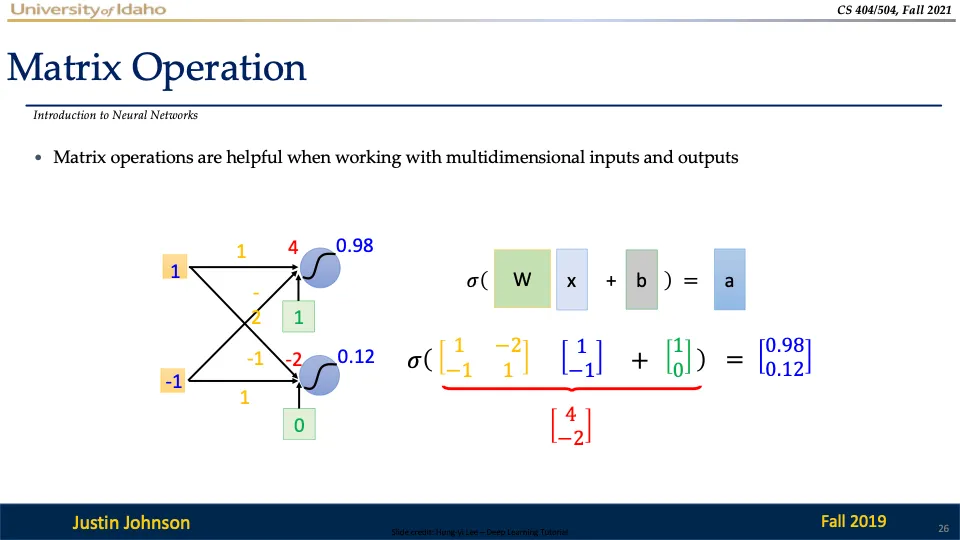
계산 방법은 이산수학에서 배우신 행렬의 곱셈을 사용하시면 됩니다!
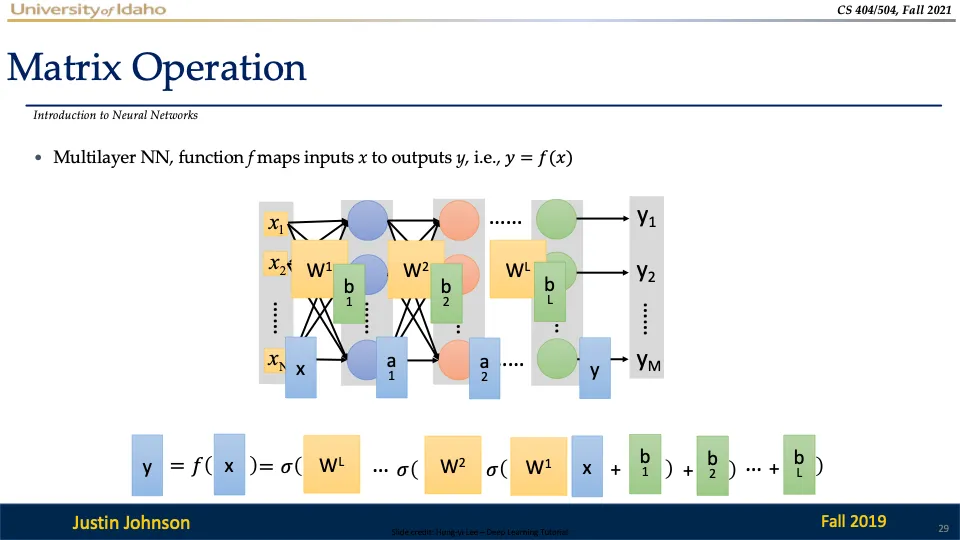
다중 계층 신경망의 전체 연산인데요,
자세히 보면 여러 계층에서 따로 따로 연산했던 것을 하나의 식으로 정리하는 것을 확인하실 수 있다~
최종적으로 신경망은 입력 x를 출력 y로 매핑하는 함수 f(x)로 표현이 되엇다!
Dropout
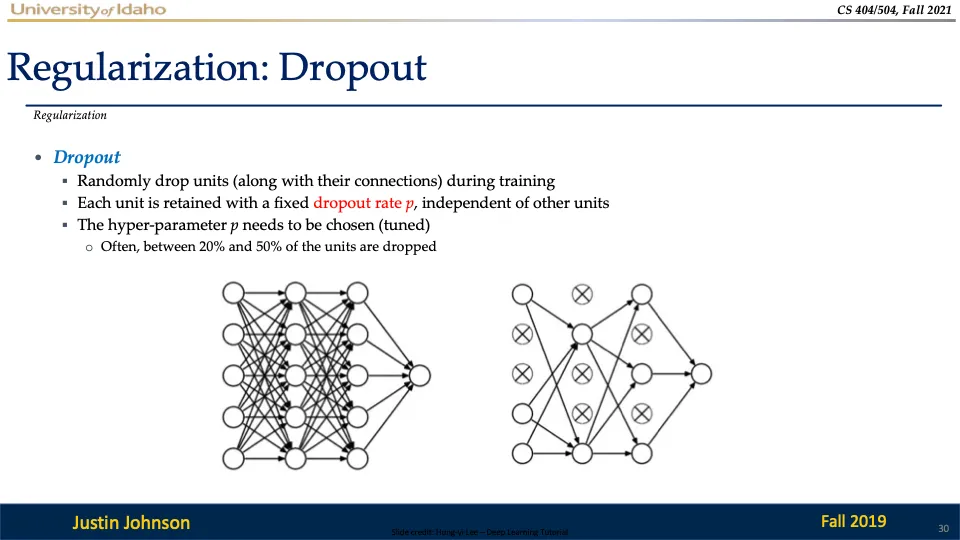
Dropout은 학습 중 임의로 일부 뉴런을 제거하고, 해당 뉴런과 연결된 가중치들을 무시하는 기법이다! (과적합 방지를 위해)
각 뉴런은 일정 확률 p에 따라 유지되며 나머지는 제거된다.
→ 유지 확률 p는 하이퍼파라미터로 20%에서 50% 사이의 뉴런을 제거하는 것이 일반적이다.
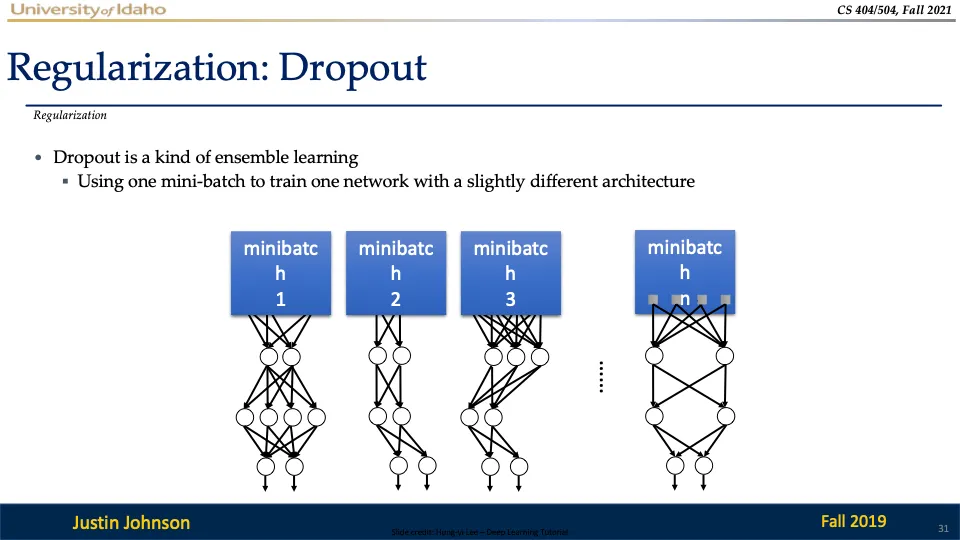
dropout은 일부 뉴런이 제거된 각 미니배치에서 다양한 서브 네트워크를 학습시키는 방법인데, 학습이 완료되면 이러한 서브 네트워크들이 결합된 형태로 동작하여 앙상블 효과를 낸다!
Early Stopping

early stopping은 모델 훈련 중, 검증세트를 사용하여 훈련을 중단할 시점을 결정하는 방법이다. (과적합 방지)
데이터셋을 훈련 세트와 검증세트로 나누고, 검증 손실이 일정한 주기 동안 개선이 되지 않으면 훈련을 멈춘다.
Activation Function

활성화 함수를 사용하지 않으면 모델은 그냥 선형 분류기에 불과하다~ 복잡한 데이터 구조를 학습할 수 없다.
여러가지 활성화 함수 중에 ReLU를 가장 많이 쓴다!
생물학적 뉴런과 인공 뉴런

인공신경망은 생물학적 뉴런을 기반으로 설계되었다.
'Computer Vision' 카테고리의 다른 글
| [컴퓨터비전] Convolutional Networks (0) | 2024.12.22 |
|---|---|
| [컴퓨터비전] Vector Backpropagation (1) | 2024.12.22 |
| [컴퓨터비전] Backpropagation (2) | 2024.12.20 |
| [컴퓨터비전] DNN(Deep Neural Network) (0) | 2024.12.19 |
| [컴퓨터비전] Linear Classifiers (0) | 2024.12.19 |
